In the world of finance, the ability to manage risk effectively is paramount. Value at Risk (VaR) is a fundamental metric that allows financial professionals to estimate potential portfolio losses, serving as a cornerstone of risk management. In this article, we explore the concept of VaR, its importance, and the methods for calculating and interpreting this crucial metric.
To Read more such Articles, Kindly visit QuantEdX.com
Understanding Value at Risk (VaR)
Value at Risk, often abbreviated as VaR, is a statistical measure used to estimate the potential loss in the value of a portfolio or investment over a specific time horizon and at a certain level of confidence. It quantifies the worst-case loss a portfolio may face under normal market conditions, typically expressed in terms of a specified confidence level (e.g., 95% or 99%).
Key Components of VaR:
- Confidence Level: VaR is defined by a confidence level, which represents the probability that the actual loss will not exceed the estimated VaR.
- Time Horizon: VaR is calculated over a specific time period, such as one day, one week, or one month, depending on the investment horizon and the nature of the portfolio.
- Portfolio Value: VaR estimates are calculated based on the current or expected future value of a portfolio, considering the composition of assets and their correlations.
Click here to read more about Conditional Value at Risk
The VaR Calculation Process
- Data Collection: Gather historical or simulated data on asset returns and market conditions relevant to the portfolio.
- Determine Confidence Level: Choose a confidence level that reflects the risk tolerance of the investor or institution.
- Select Time Horizon: Define the time horizon over which VaR will be calculated.
- Calculate Portfolio Returns: Using the data, compute the returns of the portfolio over the chosen time horizon.
- Order Returns: Arrange the portfolio returns in ascending order, from the smallest loss to the largest gain.
- Identify VaR: Identify the return corresponding to the chosen confidence level. This value represents the VaR for the portfolio.
import yfinance as yf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm
import seaborn as sns
from scipy.optimize import minimize
# Define portfolio stocks and weights
stocks = ['AAPL', 'MSFT', 'GOOGL', 'AMZN', 'TSLA', 'META', 'NFLX', 'NVDA', 'AMD', 'INTC'] # Expanded list of stock symbols
# Download historical data
def get_stock_data(tickers, start_date, end_date):
data = yf.download(tickers, start=start_date, end=end_date)
return data['Adj Close']
# Calculate daily returns
def calculate_returns(data):
returns = data.pct_change().dropna()
return returns
# Calculate portfolio returns
def calculate_portfolio_returns(returns, weights):
portfolio_returns = returns.dot(weights)
return portfolio_returns
# Calculate VaR
def calculate_var(returns, confidence_level=0.95):
sorted_returns = returns.sort_values()
index = int((1 - confidence_level) * len(sorted_returns))
var_value = sorted_returns.iloc[index]
return var_value
# Calculate Expected Shortfall (ES)
def calculate_es(returns, confidence_level=0.95):
var_value = calculate_var(returns, confidence_level)
es = returns[returns <= var_value].mean()
return es
# Define parameters
start_date = '2023-01-01'
end_date = '2024-01-01'
confidence_levels = [0.90, 0.95, 0.99] # Different confidence levels
# Get stock data
data = get_stock_data(stocks, start_date, end_date)
# Calculate returns
returns = calculate_returns(data)
# Portfolio optimization functions
def portfolio_performance(weights, returns):
portfolio_returns = calculate_portfolio_returns(returns, weights)
return portfolio_returns.mean(), portfolio_returns.std()
def min_variance(weights, returns):
_, std_dev = portfolio_performance(weights, returns)
return std_dev
def negative_sharpe_ratio(weights, returns, risk_free_rate=0.0):
mean, std_dev = portfolio_performance(weights, returns)
return -(mean - risk_free_rate) / std_dev
def optimize_portfolio(returns, method='min_variance'):
num_assets = len(returns.columns)
initial_weights = np.array(num_assets * [1. / num_assets])
constraints = ({'type': 'eq', 'fun': lambda w: np.sum(w) - 1})
bounds = tuple((0, 1) for _ in range(num_assets))
if method == 'min_variance':
result = minimize(min_variance, initial_weights, args=(returns,), method='SLSQP', bounds=bounds, constraints=constraints)
elif method == 'max_sharpe_ratio':
result = minimize(negative_sharpe_ratio, initial_weights, args=(returns,), method='SLSQP', bounds=bounds, constraints=constraints)
return result.x
# Optimize portfolios
methods = ['equal_weight', 'min_variance', 'max_sharpe_ratio']
portfolio_metrics = []
portfolio_weights = []
for method in methods:
if method == 'equal_weight':
weights = np.array(len(stocks) * [1. / len(stocks)])
else:
weights = optimize_portfolio(returns, method=method)
portfolio_returns = calculate_portfolio_returns(returns, weights)
mean_return = portfolio_returns.mean()
std_dev = portfolio_returns.std()
metrics = {'Method': method,
'Mean Return': mean_return,
'Standard Deviation': std_dev}
for cl in confidence_levels:
var_value = calculate_var(portfolio_returns, cl)
es_value = calculate_es(portfolio_returns, cl)
metrics[f'VaR at {int(cl*100)}%'] = var_value
metrics[f'ES at {int(cl*100)}%'] = es_value
portfolio_metrics.append(metrics)
portfolio_weights.append(weights)
# Convert metrics and weights to DataFrames
metrics_df = pd.DataFrame(portfolio_metrics)
weights_df = pd.DataFrame(portfolio_weights, columns=stocks, index=methods)
# Print DataFrames
print("Portfolio Metrics:")
display(metrics_df)
print("\nPortfolio Weights:")
display(weights_df)
# Plot portfolio returns distributions in subplots
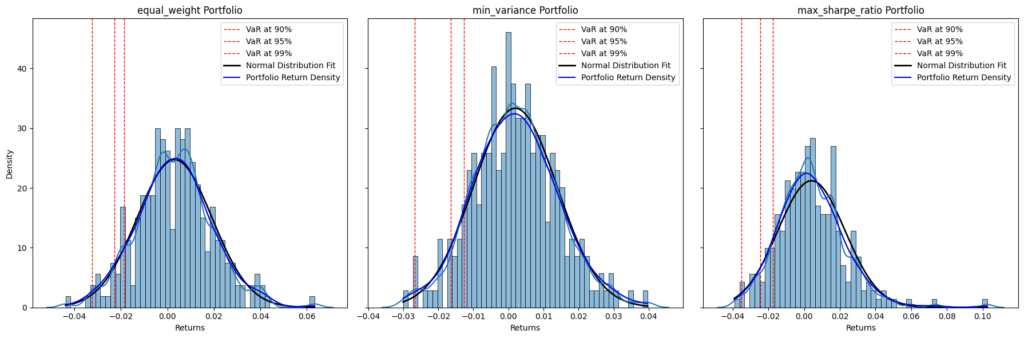
fig, axs = plt.subplots(1, 3, figsize=(18, 6), sharey=True)
optimized_portfolios = {
'equal_weight': calculate_portfolio_returns(returns, portfolio_weights[0]),
'min_variance': calculate_portfolio_returns(returns, portfolio_weights[1]),
'max_sharpe_ratio': calculate_portfolio_returns(returns, portfolio_weights[2])
}
for i, (method, returns) in enumerate(optimized_portfolios.items()):
ax = axs[i]
sns.histplot(returns, bins=50, kde=True, ax=ax, edgecolor='k', stat='density')
# Plot VaR lines for each portfolio
for cl in confidence_levels:
var_value = calculate_var(returns, cl)
ax.axvline(var_value, color='r', linestyle='dashed', linewidth=1, label=f'VaR at {int(cl*100)}%')
# Plot normal distribution
mean = returns.mean()
std_dev = returns.std()
xmin, xmax = returns.min(), returns.max()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mean, std_dev)
ax.plot(x, p, 'k', linewidth=2, label='Normal Distribution Fit')
# Plot portfolio return distribution curve
density = sns.kdeplot(returns, bw_adjust=0.5, ax=ax).get_lines()[0].get_data()
ax.plot(density[0], density[1], label='Portfolio Return Density', color='blue')
ax.set_title(f'{method} Portfolio')
ax.set_xlabel('Returns')
ax.set_ylabel('Density')
ax.legend()
plt.tight_layout()
plt.show()


Applications of VaR
- Risk Management: VaR is a vital tool for managing and monitoring risk in portfolios, enabling investors and institutions to set risk limits and assess the impact of potential losses.
- Portfolio Optimization: Portfolio managers use VaR to optimize asset allocation, ensuring that portfolios are aligned with investors’ risk preferences.
- Regulatory Compliance: Many financial regulators and institutions use VaR as a benchmark to assess capital adequacy and compliance with risk limits.
- Investment Decision-Making: Investors use VaR to make informed decisions about asset selection, diversification, and risk mitigation.
Challenges and Considerations
- Assumptions: VaR calculations rely on several assumptions, including the normal distribution of asset returns, which may not always hold true in real markets.
- Data Quality: The accuracy of VaR estimates depends on the quality and relevance of historical data.
- Tail Risk: VaR does not provide insights into extreme tail events, which can be a limitation in situations of severe market stress.
Conclusion
Value at Risk (VaR) is a pivotal metric in the world of finance, allowing investors and institutions to quantify the potential loss in the value of their portfolios with a specified level of confidence. By understanding VaR and its calculation methods, financial professionals can make informed decisions, manage risk effectively, and optimize investment portfolios. As markets continue to evolve, VaR remains a foundational tool for navigating the complexities of financial risk management.