Value at Risk, often abbreviated as VaR, is a vital concept in risk management, financial modeling, and decision-making. It provides a statistical measure of the potential loss an investment or portfolio might experience over a specified time horizon, at a given confidence level. This article provides an in-depth exploration of VaR, including its history, mathematical formulas, types, meanings, and how to interpret its significance.
History of Value at Risk
The concept of VaR traces its roots to the financial industry’s increasing need for risk assessment and management. It gained prominence in the late 20th century as a result of the following developments:
- The 1980s: The rapid growth of financial markets and the increasing complexity of financial products created a need for more sophisticated risk management techniques.
- 1990s: Financial institutions, particularly banks, began to adopt VaR as a risk measurement tool. It was endorsed by regulatory bodies, such as the Basel Committee on Banking Supervision, leading to its widespread use in the industry.
The Mathematical Foundation of Value at Risk (VaR)
At the core of VaR is a probability-based approach, often relying on statistical and mathematical models. Several formulas are used to calculate VaR, each tailored to different applications. Here, we present some of the most fundamental ones in LaTeX code:
- Parametric VaR (Normal Distribution):
VaR = \mu + z \sigma
Where:
- VaR is the Value at Risk.
- μ is the mean return.
- z is the critical value (often obtained from a standard normal distribution table) corresponding to the desired confidence level.
- σ is the standard deviation of returns.
- Historical VaR:
VaR = -P_t \quad \text{where} \quad P_t \text{ is the } x^{th} \text{ percentile of historical returns}- Monte Carlo VaR:
This approach involves generating thousands of scenarios, simulating portfolio returns, and finding the xth percentile of the resulting distribution.
Types of Value at Risk (VaR)
- Marginal VaR: This type of VaR focuses on the risk contributed by individual assets within a portfolio. It measures the potential loss associated with each asset if held in isolation, considering the rest of the portfolio remains unchanged. Marginal VaR helps in understanding which assets have the most significant impact on the overall portfolio risk.
- Component VaR: Component VaR extends the idea of marginal VaR to segments or categories within a portfolio. Instead of isolating individual assets, it assesses the risk contributed by specific groups or sectors of the portfolio. This type of VaR is valuable for diversification analysis and managing risks associated with different investment categories.
- Backtesting VaR: Backtesting VaR is a critical component of VaR risk management. It involves comparing the actual portfolio losses with the VaR estimates. By examining the frequency and severity of losses that exceed VaR predictions, financial institutions and investment firms can fine-tune their risk models and ensure that VaR is a reliable measure of risk exposure.
- Stressed VaR: Stressed VaR assesses the portfolio’s risk under extreme or stressed market conditions. It helps investors and risk managers understand how the portfolio might perform during severe economic downturns or financial crises. By incorporating stressed scenarios, it provides a more comprehensive risk assessment.
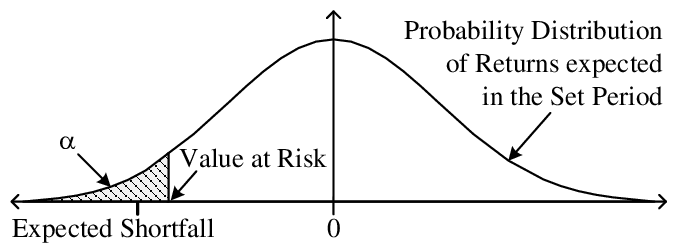
- Conditional VaR (CVaR): Also known as Expected Shortfall, CVaR goes beyond VaR by quantifying the expected loss in case the losses exceed the VaR estimate. It provides a more in-depth understanding of the tail risk of a portfolio. Unlike VaR, which only specifies a potential loss level, CVaR provides insights into the magnitude of losses beyond that point.
- Incremental VaR: Incremental VaR assesses the additional risk introduced by including a specific asset or position in a portfolio. It helps investors and portfolio managers evaluate whether adding an asset enhances or hinders the overall portfolio’s risk-return profile.
- Expected Tail Loss (ETL): Expected Tail Loss is another extension of VaR that focuses on the tail of the distribution of returns. It calculates the average loss beyond a certain quantile, typically beyond the VaR level. ETL is particularly useful for understanding the extent of potential losses during adverse market conditions.
- Systemic Risk VaR: This type of VaR measures the risk associated with the entire financial system or market. It assesses the potential impact of systematic events or shocks on a portfolio. Systemic risk VaR helps investors prepare for market-wide disruptions and crises.
- Specific Risk VaR: Specific risk VaR concentrates on the idiosyncratic or asset-specific risk within a portfolio. It isolates the risk unique to individual assets and is valuable for managing asset-specific exposures.
- Residual Risk VaR: Residual risk VaR considers the risk remaining in a portfolio after hedging or risk mitigation strategies have been applied. It helps evaluate the effectiveness of risk-reduction measures and assesses the true residual risk of a portfolio.
Additional concepts related to Value at Risk (VaR)
Parametric VaR for a Portfolio: For a portfolio of assets, the Parametric VaR is calculated by considering the portfolio’s weighted sum of asset returns.
If Ri represents the return of asset i in the portfolio with weight wi, the formula is:
VaR = \sum_i (w_i \cdot R_i) + z \cdot \sigma_p
σp is the portfolio standard deviation.
Cornish-Fisher VaR: This formula adjusts Parametric VaR to account for skewness and kurtosis in return distributions. It provides a more accurate estimate when returns are not normally distributed.
VaR = \mu + z \sigma + \left(\frac{z^2 - 1}{6}\right) \cdot S + \left(\frac{z^3 - 3z}{24}\right) \cdot KS is the skewness of returns.
K is the kurtosis of returns.
Delta-Normal VaR: Delta-Normal VaR is used in options trading to calculate the change in the value of an option or derivative due to small changes in the underlying asset price
VaR = \Delta S \cdot N^{-1}(\alpha)ΔS is the change in the asset price.
N−1(α) is the quantile of the standard normal distribution corresponding to the desired confidence level.
Understanding the Meaning of Value at Risk (VaR)
VaR quantifies the risk of a portfolio or investment, but understanding its significance is critical. Consider the following key points:
- Confidence Level: VaR is calculated at a specific confidence level, such as 95% or 99%. A 95% VaR indicates that there is a 5% chance of experiencing losses greater than the VaR estimate over the specified time horizon.
- Time Horizon: The time period over which VaR is measured is a crucial factor. A one-day VaR measures the potential loss over a single day, while longer time horizons offer insights into longer-term risks.
- Interpretation: VaR represents a worst-case scenario estimate. For example, if a one-day VaR is $1 million at a 95% confidence level, this implies there is a 5% chance of losing more than $1 million in a single day.
- Limitations: VaR has limitations, such as assuming normal distribution and not considering extreme events. It should be used in conjunction with other risk measures for a comprehensive risk assessment.
Conclusion
Value at Risk is a powerful tool for risk assessment and management. Its mathematical foundation, types, and interpretations offer a multifaceted perspective on potential losses. While it has become a standard in finance, it’s essential to grasp its assumptions and limitations to make informed decisions and safeguard portfolios against unforeseen risks.