Modern Portfolio Theory (MPT) is a groundbreaking concept in the world of finance that revolutionized the way investors approach risk and return. Developed by economist Harry Markowitz in the 1950s, MPT has since become a cornerstone of portfolio management. In this article, we will delve into the historical details, mathematical formulation, and key concepts related to Modern Portfolio Theory, offering a comprehensive understanding of this fundamental financial framework.
Historical Background
Modern Portfolio Theory emerged during a period of economic and financial turbulence in the mid-20th century. Harry Markowitz, in his pioneering work, sought to address the fundamental challenge faced by investors: how to maximize returns while minimizing risk. Prior to MPT, investors typically made decisions based solely on the expected returns of individual assets. However, this approach failed to account for the critical relationship between asset returns and their correlations, leading to inefficient and often risky portfolios.
Markowitz’s Mathematical Formulation
At the core of Modern Portfolio Theory lies a mathematical framework that quantifies the trade-off between risk and return. The key mathematical concept is the efficient frontier, which represents the set of portfolios that offer the maximum expected return for a given level of risk or the minimum risk for a given level of expected return.
To Read more about Arbitrage Pricing Model (APT), please visit – A Guide to Arbitrage Pricing Model
Key Concepts in Modern Portfolio Theory
Risk Diversification
Risk diversification is a crucial concept in finance and investment, which aims to minimize the overall risk associated with holding a portfolio of investments by spreading resources across different assets or asset classes. This strategy is grounded in the idea that different assets often react differently to economic and market events. By holding a variety of investments, investors can reduce the impact of poor performance in any single asset on the overall portfolio.
Mathematically, risk diversification can be expressed using the concept of portfolio variance. The formula for calculating the variance of a portfolio consisting of two assets (Asset 1 and Asset 2) is as follows:
\text{Portfolio Variance} (\sigma^2_p) = w_1^2 \cdot \sigma^2_1 + w_2^2 \cdot \sigma^2_2 + 2 \cdot w_1 \cdot w_2 \cdot \text{Cov}(\text{Asset 1, Asset 2})
\begin{align*}
& \sigma^2_p : \text{Portfolio Variance} \\
& w_1 : \text{Weight of Asset 1 in the Portfolio} \\
& w_2 : \text{Weight of Asset 2 in the Portfolio} \\
& \sigma^2_1 : \text{Variance of Asset 1} \\
& \sigma^2_2 : \text{Variance of Asset 2} \\
& \text{Cov}(\text{Asset 1, Asset 2}) : \text{Covariance between Asset 1 and Asset 2}
\end{align*}
The portfolio variance formula highlights how the diversification effect works. When assets have a positive covariance (they tend to move in the same direction), the third term in the formula (the covariance term) increases the portfolio variance. However, when assets have a negative or low covariance (they move differently or in opposite directions), the covariance term helps reduce the portfolio variance. Therefore, by holding assets with low or negative correlations, investors can achieve a more diversified portfolio with lower overall risk.
In practice, this mathematical representation extends to portfolios with more than two assets, where the formula becomes more complex due to the need to account for the covariances between all pairs of assets in the portfolio. Modern portfolio optimization tools and software use these principles to construct well-diversified portfolios that aim to achieve the desired risk-return trade-offs.
To Read More Such Articles, please visit QuantEdX.com
Efficient Frontier
The efficient frontier is a fundamental concept in Modern Portfolio Theory (MPT) that plays a central role in helping investors make informed decisions about their portfolios
The efficient frontier is a graph or curve that represents a set of portfolios that achieve the highest expected return for a given level of risk or the lowest risk for a given level of expected return. In essence, it illustrates the trade-off between risk and return that investors face when constructing their portfolios.
The efficient frontier demonstrates the principle that, in general, higher expected returns come with higher levels of risk. However, it also highlights that there is no single “optimal” portfolio; instead, there is a range of portfolios that offer various risk-return combinations along the curve.
The risk component of the efficient frontier is typically measured using standard deviation or variance. Standard deviation quantifies the volatility or dispersion of returns, with higher values indicating greater risk. By optimizing the portfolio to minimize standard deviation, investors aim to minimize risk.
The process of constructing a portfolio on the efficient frontier is known as portfolio optimization. It involves determining the allocation of assets (weights) in the portfolio to achieve a specific risk-return target.
A key result related to the efficient frontier is the Two-Fund Separation Theorem. It states that investors can choose any combination of a risk-free asset (e.g., government bonds) and a portfolio on the efficient frontier to meet their risk-return preferences. This separation simplifies the investment decision by separating the choice of risky assets from the choice of risk-free assets.
The point on the efficient frontier that represents the entire market is known as the market portfolio. This is the portfolio that includes all investable assets and is often used as a benchmark in portfolio construction.
Investors’ preferences for risk and return are unique, and the efficient frontier allows them to choose portfolios that align with their utility function. A utility function quantifies an investor’s preferences and risk tolerance, helping them select the optimal portfolio.
The shape and location of the efficient frontier can change over time due to shifts in market conditions, asset returns, and correlations. Therefore, it’s essential for investors to periodically review and adjust their portfolios to stay on or near the efficient frontier.
E(R_p) = \text{Minimize } \sigma_p \text{ subject to } \sum_{i=1}^{n} w_i = 1
\begin{align*}
E(R_p) & : \text{Expected Return of the Portfolio}\\
\sigma_p & : \text{Standard Deviation (Volatility) of the Portfolio}\\
w_i & : \text{Weight of Asset } i \text{ in the Portfolio}\\
n & : \text{Total number of assets in the Portfolio}
\end{align*}
Covariance
Covariance is a statistical measure that quantifies the degree to which two random variables change together. In simpler terms, it tells us how two variables move in relation to each other. It’s an important concept in statistics and finance, particularly in portfolio theory and risk management. Here’s an explanation of covariance:
Covariance measures the directional relationship between two random variables. There are three possible scenarios:
- Positive Covariance: When the values of one variable tend to increase as the values of the other variable increase and decrease as the other variable decreases, the covariance is positive. This suggests a positive relationship between the variables, meaning they tend to move in the same direction.
- Negative Covariance: When the values of one variable tend to decrease as the values of the other variable increase, and vice versa, the covariance is negative. This indicates a negative relationship, meaning the variables tend to move in opposite directions.
- Zero Covariance: When changes in one variable have no effect on the other variable, the covariance is close to zero. This suggests little to no linear relationship between the variables.
\text{Cov}(X, Y) = \frac{\sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y})}{n-1}
\begin{align*}
\text{Cov}(X, Y) & : \text{The covariance between random variables } X \text{ and } Y.\\
X & : \text{The first random variable.}\\
Y & : \text{The second random variable.}\\
X_i & : \text{An individual data point or observation of random variable } X.\\
Y_i & : \text{An individual data point or observation of random variable } Y.\\
\bar{X} & : \text{The mean (average) of random variable } X.\\
\bar{Y} & : \text{The mean (average) of random variable } Y.\\
n & : \text{The number of data points or observations in the sample.}
\end{align*}
Correlation
It is a statistical measure that quantifies the strength and direction of the linear relationship between two continuous random variables. It tells us how closely and in what direction two variables tend to move together. Correlation is expressed as the correlation coefficient, often denoted as ρ (rho) for the population correlation or r for the sample correlation.
The mathematical formula for the sample correlation coefficient (r) is as follows:
r = \frac{\sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^n (X_i - \bar{X})^2 \sum_{i=1}^n (Y_i - \bar{Y})^2}}
r = \text{Sample Correlation Coefficient}\\
X_i, Y_i = \text{Individual data points for } X \text{ and } Y\\
\bar{X}, \bar{Y} = \text{Means (average values) of } X \text{ and } Y\\
n = \text{Number of data points in the sample}\\
Capital Allocation Line (CAL)
The Capital Allocation Line (CAL) is a concept in finance that represents the trade-off between risk and return that an investor can achieve by constructing a portfolio that combines a risk-free asset (such as Treasury bills) and a risky asset (such as stocks or bonds). The CAL is a graphical representation of the different risk-return profiles available to investors when they allocate their investments between these two types of assets.
Here’s an explanation of the CAL and its mathematical formulation:
E(R_p) = R_f + \frac{E(R_m) - R_f}{\sigma_m} \cdot \sigma_p The CAL essentially shows the relationship between the expected return (E(Rp)) and the risk (σ) for portfolios that vary in their allocation between the risk-free asset and the risky asset. Investors can choose a point on the CAL that matches their risk tolerance. Portfolios located to the left of the CAL are suboptimal because they provide lower returns for a given level of risk. Portfolios on the CAL itself are considered efficient portfolios as they provide the highest return for a given level of risk.
Sharpe Ratio
The Sharpe Ratio, named after its creator William F. Sharpe, is a widely used measure in finance to evaluate the risk-adjusted return of an investment or portfolio. It helps investors assess whether the returns earned on an investment are sufficient to compensate for the risk taken.
Mathematical Formulation:
The Sharpe Ratio is calculated using the following formula:
\text{Sharpe Ratio (SR)} = \frac{R_p - R_f}{\sigma_p}
\begin{align*}
\text{Sharpe Ratio (SR)} & : \text{A measure of the risk-adjusted return of a portfolio.}\\
R_p & : \text{The expected return of the portfolio.}\\
R_f & : \text{The risk-free rate of return}\\
\sigma_p & : \text{The standard deviation (volatility) of the portfolio's returns}
\end{align*}
Explanation:
The Sharpe Ratio formula consists of two main components:
- Excess Return: This represents the difference between the expected return of the portfolio (Rp) and the risk-free rate (Rf). It quantifies how much the investment or portfolio has earned beyond the risk-free return. This excess return is often referred to as the “risk premium” and is a measure of the return investors are earning for taking on the additional risk associated with the investment.
- Risk (σ): This is represented by the standard deviation of the portfolio’s returns (σ). It measures the volatility or variability of the portfolio’s returns. A higher standard deviation implies greater risk.
The Sharpe Ratio essentially tells you how much additional return you’re getting for each unit of risk you’re taking on. A higher Sharpe Ratio indicates a better risk-adjusted return because it means you’re earning more return for the same amount of risk, or equivalently, you’re taking on less risk for the same level of return.
In practice, investors and fund managers often use the Sharpe Ratio to compare the risk-adjusted performance of different investments or portfolios. They prefer investments or portfolios with higher Sharpe Ratios because they provide better compensation for the risk taken. However, it’s important to note that the Sharpe Ratio is just one measure, and investors should consider other factors, such as their risk tolerance and investment goals when making investment decisions.
Minimum Variance Portfolio
The Minimum Variance Portfolio (MVP) is a concept in portfolio theory in finance. It represents a portfolio or combination of assets that is constructed to minimize the portfolio’s overall risk or volatility, subject to a specific set of constraints. In other words, the goal of the Minimum Variance Portfolio is to create an investment portfolio that provides the lowest possible level of risk among all possible portfolios with the given assets.
The primary objective of the Minimum Variance Portfolio is to achieve the lowest possible variance or standard deviation of returns. Variance is a measure of the spread or volatility of returns, so minimizing it implies reducing the portfolio’s overall risk.
The MVP is determined through mathematical optimization techniques, typically involving quadratic programming. The goal is to find the weights of each asset in the portfolio that will lead to the lowest portfolio variance while satisfying certain constraints.
Constraints are imposed to ensure that the portfolio remains feasible and practical. Common constraints include a budget constraint (the sum of the weights equals 1), which ensures that the entire investment is allocated, and sometimes constraints on individual asset weights (e.g., no short selling, which means weights cannot be negative).
The MVP is essentially a well-diversified portfolio. It spreads investments across different assets in a way that minimizes the impact of individual asset price fluctuations on the overall portfolio. By holding assets with low or negative correlations, the MVP further reduces the portfolio’s overall risk.
While the Minimum Variance Portfolio aims to minimize risk, it may not necessarily offer the highest returns. Investors often face a trade-off between risk and return. Portfolios with higher expected returns usually come with higher levels of risk, and vice versa. The MVP represents the endpoint of this trade-off for the given set of assets.
The Minimum Variance Portfolio concept is fundamental in modern portfolio theory (MPT) and asset allocation. It provides a starting point for investors to consider their risk tolerance and objectives. Many investors use the MVP as a building block and then adjust their portfolios based on their specific return goals and risk preferences.
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
# Step 1: Download historical price data for a portfolio of stocks
tickers = ['AAPL', 'MSFT', 'GOOGL', 'TSLA', 'AMZN']
data = yf.download(tickers, start='2020-01-01', end='2023-01-01')['Adj Close']
# Step 2: Calculate daily returns
returns = data.pct_change().dropna()
# Step 3: Calculate expected returns and covariance matrix
mean_returns = returns.mean()
cov_matrix = returns.cov()
# Step 4: Set the number of portfolios to simulate
num_portfolios = 10000
# Step 5: Initialize arrays to store portfolio performance metrics
results = np.zeros((3, num_portfolios))
weights_record = []
# Step 6: Run simulations to create random portfolios
for i in range(num_portfolios):
weights = np.random.random(len(tickers))
weights /= np.sum(weights)
# Portfolio return and volatility
portfolio_return = np.sum(weights * mean_returns) * 252 # Annualized return
portfolio_volatility = np.sqrt(np.dot(weights.T, np.dot(cov_matrix * 252, weights))) # Annualized risk
# Sharpe Ratio (assume risk-free rate = 0)
sharpe_ratio = portfolio_return / portfolio_volatility
# Store the results
results[0, i] = portfolio_return
results[1, i] = portfolio_volatility
results[2, i] = sharpe_ratio
weights_record.append(weights)
# Step 7: Create DataFrame of the results
portfolios = pd.DataFrame({
'Return': results[0],
'Volatility': results[1],
'Sharpe Ratio': results[2]
})
# Step 8: Find the portfolio with the maximum Sharpe Ratio and minimum volatility
max_sharpe_idx = np.argmax(results[2])
min_volatility_idx = np.argmin(results[1])
# Step 9: Plot the efficient frontier
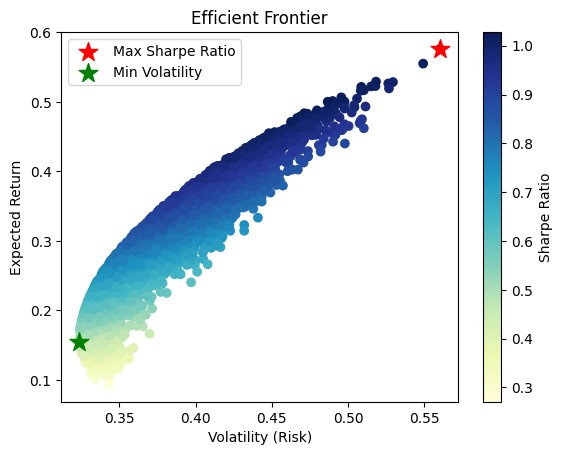
plt.scatter(portfolios['Volatility'], portfolios['Return'], c=portfolios['Sharpe Ratio'], cmap='YlGnBu', marker='o')
plt.title('Efficient Frontier')
plt.xlabel('Volatility (Risk)')
plt.ylabel('Expected Return')
plt.colorbar(label='Sharpe Ratio')
# Highlight portfolios with max Sharpe and minimum volatility
plt.scatter(portfolios.iloc[max_sharpe_idx]['Volatility'], portfolios.iloc[max_sharpe_idx]['Return'], marker='*', color='r', s=200, label='Max Sharpe Ratio')
plt.scatter(portfolios.iloc[min_volatility_idx]['Volatility'], portfolios.iloc[min_volatility_idx]['Return'], marker='*', color='g', s=200, label='Min Volatility')
plt.legend()
plt.show()
# Display the optimal portfolio with maximum Sharpe Ratio
max_sharpe_portfolio = portfolios.iloc[max_sharpe_idx]
min_vol_portfolio = portfolios.iloc[min_volatility_idx]
print("\nPortfolio with maximum Sharpe Ratio:")
print("Return:", max_sharpe_portfolio['Return'])
print("Volatility:", max_sharpe_portfolio['Volatility'])
print("Sharpe Ratio:", max_sharpe_portfolio['Sharpe Ratio'])
print("\nPortfolio with minimum volatility:")
print("Return:", min_vol_portfolio['Return'])
print("Volatility:", min_vol_portfolio['Volatility'])
Capital Market Line (CML)
The primary objective of the CML is to illustrate how investors can combine a risk-free asset (typically represented by government bonds) with a portfolio of risky assets (such as stocks) to achieve the optimal balance between risk and return.
The CML assumes the existence of a risk-free asset, typically represented by government bonds. This asset is considered free from default risk and is used as a reference point for constructing portfolios.
The CML plots different portfolios on a graph, with risk (usually measured as standard deviation or volatility) on the x-axis and expected return on the y-axis. These portfolios are formed by varying the allocation between the risk-free asset and the risky portfolio.
The line represents the “efficient frontier” of portfolios that offer the highest expected returns for a given level of risk. It’s the upper boundary of the set of all feasible portfolios. Portfolios lying on or above the CML are considered efficient because they offer higher returns than the risk-free asset for the same level of risk.
The slope of the CML is important. It indicates the additional expected return an investor can earn for each additional unit of risk (standard deviation) taken. The steeper the slope, the greater the expected return per unit of risk.
The point at which the CML is tangent to the efficient frontier represents the optimal portfolio for an investor. This is the portfolio that maximizes the risk-adjusted return, often measured using the Sharpe Ratio. It’s the point where an investor combines the risk-free asset with the risky portfolio to achieve the best trade-off between risk and return based on their risk tolerance.
The CML is a critical concept in portfolio construction and asset allocation. It guides investors in determining the optimal mix of risky assets and a risk-free asset in their portfolios, based on their individual risk preferences and investment objectives.
Systematic Risk
Systematic risk, often referred to as market risk or undiversifiable risk, is a type of risk that is inherent to the entire market or an entire asset class. It cannot be eliminated through diversification because it affects all investments within a particular market or asset class. Systematic risk is driven by external factors and events that impact the broader economy and financial markets. Here’s a more detailed explanation:
Characteristics of Systematic Risk:
- Market-Wide Impact: Systematic risk affects all investments within a given market or asset class simultaneously. This means that when a systematic event occurs, such as an economic recession or a significant geopolitical event, the prices of most or all assets within that market tend to move in the same direction.
- Cannot be Diversified Away: One of the key characteristics of systematic risk is that it cannot be eliminated or significantly reduced through diversification. Diversification, which involves spreading investments across different asset classes or securities, can help reduce unsystematic or idiosyncratic risk (i.e., risks specific to individual assets), but it cannot mitigate systematic risk.
- Macroeconomic Factors: Systematic risk is driven by macroeconomic factors and events that impact the overall economy. These factors include changes in interest rates, inflation, GDP growth, political events, and global economic conditions.
- Examples of Systematic Risk: Some common examples of systematic risk include:
- Market Risk: Fluctuations in the overall stock market due to economic conditions.
- Interest Rate Risk: Changes in interest rates that affect bond prices and borrowing costs.
- Inflation Risk: Rising inflation erodes the real value of investments.
- Currency Risk: Changes in exchange rates can impact international investments.
- Political Risk: Government policies, regulations, or geopolitical events can affect markets.
- Measured by Beta: In finance, systematic risk is often measured using beta (β), a metric that quantifies an asset’s sensitivity to overall market movements. An asset with a beta of 1 moves in line with the market, while a beta greater than 1 indicates higher volatility, and a beta less than 1 indicates lower volatility compared to the market.
Importance of Systematic Risk:
Understanding systematic risk is crucial for investors and portfolio managers because it helps them assess the overall risk exposure of their portfolios. By recognizing that certain events or economic conditions can impact all investments within a market, investors can make informed decisions about asset allocation, risk management, and diversification strategies.
In summary, systematic risk is a fundamental component of investment risk that is associated with factors affecting entire markets or asset classes. It cannot be eliminated through diversification and is influenced by macroeconomic variables and events that impact the broader economy and financial markets.
Unsystematic Risk
Unsystematic risk, often referred to as specific risk, unique risk, or idiosyncratic risk, is a type of investment risk that is specific to a particular company, industry, or asset. It is distinct from systematic risk, which affects the entire market or asset class. Unsystematic risk can be reduced or eliminated through diversification because it is associated with factors or events that are unique to individual assets or small groups of assets. Here’s a more detailed explanation:
Characteristics of Unsystematic Risk:
- Asset-Specific: Unsystematic risk is associated with factors or events that affect a specific company, industry, or asset but do not impact the entire market. These factors can include company-specific events such as management changes, product recalls, or lawsuits.
- Diversifiable: Because unsystematic risk is specific to individual assets or small groups of assets, it can be reduced or eliminated through diversification. Diversification involves spreading investments across different assets or asset classes to mitigate the impact of unsystematic risk. By holding a well-diversified portfolio, investors can reduce their exposure to the specific risks associated with individual assets.
- Examples of Unsystematic Risk: Some common examples of unsystematic risk include:
- Company-Specific Risk: Risks associated with a particular company, such as management issues, supply chain disruptions, or labor strikes.
- Industry-Specific Risk: Risks associated with an entire industry, such as regulatory changes affecting pharmaceutical companies or commodity price fluctuations affecting energy companies.
- Credit Risk: The risk that a borrower (e.g., a bond issuer) will default on its obligations.
- Liquidity Risk: The risk of not being able to buy or sell an asset at the desired price due to low trading volume or market conditions specific to that asset.
- Reducible Through Diversification: The key strategy for mitigating unsystematic risk is diversification. By holding a diversified portfolio of assets from different sectors and industries, investors can reduce their exposure to individual asset-specific risks. When one asset in the portfolio experiences negative news or events, it is offset by the positive performance of other assets.
- Beta Excludes Unsystematic Risk: In financial analysis, beta (β) is used to measure an asset’s sensitivity to overall market movements, but it excludes unsystematic risk. Beta reflects only the systematic risk associated with an asset, which means that the asset’s unique or specific risks are not considered in the calculation of beta.
Importance of Unsystematic Risk:
Understanding unsystematic risk is essential for investors because it highlights the importance of diversification as a risk management strategy. By diversifying their portfolios, investors can reduce the impact of asset-specific risks, thereby achieving a more balanced and stable investment portfolio.
In summary, unsystematic risk is specific to individual assets or small groups of assets and can be mitigated through diversification. It encompasses risks unique to particular companies, industries, or assets and is a key consideration for investors when constructing portfolios and managing risk.
Alpha and Beta
Alpha and beta are key concepts in finance and investment analysis, often used to assess the performance and risk of investment portfolios or individual assets. They help investors understand how an investment or portfolio has performed relative to a benchmark (usually a market index) and whether it provides value beyond what would be expected given its level of risk. Here’s an explanation of alpha and beta:
Alpha:
- Definition: Alpha (α) is a measure of an investment’s or portfolio’s risk-adjusted performance. It quantifies how an investment has performed relative to a chosen benchmark after adjusting for its level of risk.
- Interpretation:
- A positive alpha indicates that the investment or portfolio has outperformed the benchmark after considering its risk.
- A negative alpha suggests underperformance relative to the benchmark, even after accounting for risk.
- A zero alpha means the investment performed in line with what would be expected given its risk.
- Significance: Alpha is important because it assesses the skill of the portfolio manager or the investment strategy. A positive alpha may indicate superior investment decisions or the ability to generate excess returns, while a negative alpha may suggest poor investment decisions or higher risk than the benchmark.
Beta:
- Definition: Beta (β) is a measure of an investment’s or portfolio’s sensitivity to overall market movements. It quantifies how much an asset’s returns are expected to move in relation to changes in a market index, typically the overall stock market.
- Interpretation:
- A beta of 1 indicates that the investment tends to move in line with the market.
- A beta greater than 1 suggests that the investment is more volatile than the market (amplifies market movements).
- A beta less than 1 indicates that the investment is less volatile than the market (smoother movements).
- Significance: Beta helps investors understand the systematic risk associated with an investment. Assets with higher betas tend to be riskier because they have a stronger connection to market movements. Beta is often used to assess how a particular investment or portfolio contributes to overall portfolio risk.
Relationship Between Alpha and Beta:
- Alpha and beta are often considered together to evaluate an investment’s risk-return profile.
- A positive alpha indicates that an investment has outperformed its expected return based on its beta, suggesting it provides value beyond market performance.
- A negative alpha implies underperformance, meaning the investment has failed to meet expectations given its market sensitivity (beta).
In summary, alpha measures an investment’s risk-adjusted performance relative to a benchmark, while beta quantifies its sensitivity to market movements. Both metrics are valuable tools for investors and portfolio managers in evaluating investments and constructing well-balanced portfolios.
Markowitz Efficient Set
The Markowitz Efficient Set, also known as the Efficient Frontier, is a fundamental concept in modern portfolio theory (MPT), developed by Nobel laureate Harry Markowitz. It represents a set of investment portfolios that provide the maximum possible expected return for a given level of risk or the minimum possible risk for a given level of expected return. In other words, it’s a collection of portfolios that offer the best risk-return trade-offs.
Here’s an explanation of the Markowitz Efficient Set:
The primary objective of the Markowitz Efficient Set is to help investors construct portfolios that achieve the highest possible return for a given level of risk or the lowest possible risk for a given level of return.
The concept is based on the idea that by diversifying a portfolio—investing in a mix of assets with different risk-return profiles—investors can optimize their portfolios to achieve better risk-adjusted returns. Diversification helps reduce unsystematic or idiosyncratic risk (specific to individual assets) while retaining exposure to systematic risk (market-related risk).
The Efficient Frontier is determined through mathematical optimization techniques. The goal is to identify the combination of assets or asset weights that maximize the expected return for a given level of risk. This process involves calculating the expected return, risk (usually measured as standard deviation or volatility), and correlation among assets.
The Efficient Frontier is often represented graphically as a curve on a risk-return graph. On the x-axis, you have the portfolio’s risk (volatility), and on the y-axis, you have the portfolio’s expected return. Each point on the curve represents a different portfolio, with the portfolios to the left of the curve considered inefficient (suboptimal) because they offer lower returns for the same level of risk.
The point on the Efficient Frontier that aligns with an investor’s risk tolerance and return objective represents the optimal portfolio for that investor. It’s the portfolio that strikes the best balance between risk and return based on their preferences.
The Markowitz Efficient Set illustrates the trade-off between risk and return. As you move along the curve to the right, you increase your expected return but also take on more risk. Conversely, moving to the left reduces risk but at the cost of lower expected returns.
The Efficient Frontier is a critical tool for portfolio construction and asset allocation. It helps investors and portfolio managers make informed decisions about how to allocate their investments among different asset classes to achieve their financial goals while managing risk.
In summary, the Markowitz Efficient Set, or Efficient Frontier, is a fundamental concept in portfolio theory that helps investors build diversified portfolios that offer the best risk-return trade-offs. It provides a framework for optimizing investment portfolios based on individual risk tolerance and return objectives.
FAQs
- Is MPT still relevant today? Yes, MPT remains a cornerstone of investment theory and practice.
- Can MPT eliminate all investment risk? No, but it can help investors manage and mitigate risk effectively.
- What are the limitations of MPT? MPT assumes that market returns follow a normal distribution, which may not always hold true.
- How can I apply MPT to my portfolio? Consult a financial advisor or use portfolio optimization tools to construct a diversified portfolio.
- Does MPT consider qualitative factors like company management? No, MPT primarily focuses on quantitative factors, but qualitative analysis can complement it.
Conclusion
Modern Portfolio Theory has revolutionized the way investors approach risk and return, offering a systematic approach to portfolio construction. By understanding its historical context, mathematical foundations, and key concepts, investors can make more informed decisions and build portfolios that align with their financial goals and risk tolerance. While MPT is not without its limitations, it remains a powerful tool in the world of finance, shaping investment strategies and portfolio management to this day.